• Concentric
• Downloads

Symlateral Magic Squares

Description

These squares have complementary numbers that:

• in each octant are all symmetric about the center of their row or column
• in each octant boundary are all symmetric about the middle

See symlateral.

These can be transformed from/to concentric magic squares by repeating transform 2. Swap all pairs of rows on the top side of the square in increasing sequence, e.g., for orders 9 and 10, swap rows (1 2), (1 3), (1 4), (2 3), (2 4), (3 4).

Construction

SymlateralSquares makes these squares.

Odd Order Squares

Example Squares: Order 5, 7

The center 3x3 square can be any center of an odd concentric magic square of the same order including any aspect of the Lo Shu square.

Bones of Above Squares

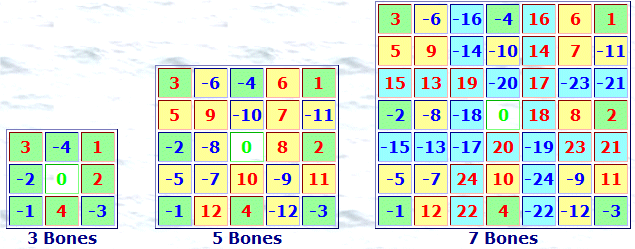
Each order n bones is conceptually made from the n-2 bones by:

• expanding the square at the middle row and middle column to make space for two new rows and columns
• filling the new rows and columns with the remaining complementary pairs such that:
  • a pair is in each of the main diagonals
  • a pair is in each of the center row and center column
  • a pair is in each top and bottom row
  • a pair is in each left and right column
  • the new rows and columns have the magic sum.

Even Order Squares

Example Squares: Order 6, 8

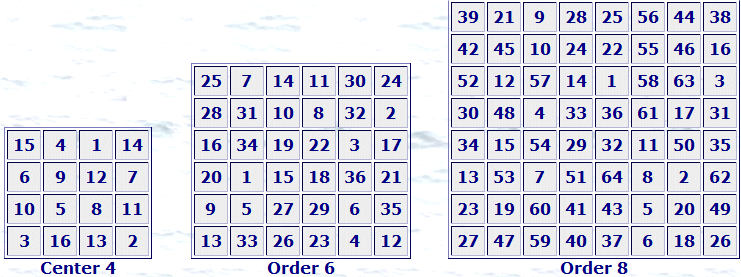
The center 4x4 square can be any center of an even concentric magic square of the same order including any aspect of the 880 order 4 squares.

Bones of Above Squares

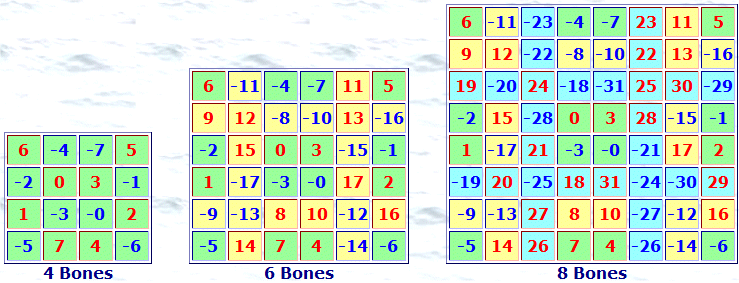
These are conceptually made as for odd order bones, but reserving two middle rows and columns here, (see octant boundaries).

Note 1: ½ has been omitted from all the bones numbers displayed here. Therefore, to convert these displayed bones numbers to the actual square numbers:

• add n²/2 + 1 to the positive numbers
• add n²/2 to the negative numbers

Note 2: Here the outside cells of the middle rows and middle columns are not middle symmetric.