Reversible Squares

Description

Reversible squares contain the numbers 1 to n² and have these features:

for the square itself and for each contained square and rectangle, one pair of diagonally opposite corner numbers has the same sum as the other pair of diagonally opposite corner numbers
in each row and column, all symmetrically opposite pairs have the same sum; for odd order squares, the row or column middle number is half that sum

Of course, these squares are not magic. However, the (pan)diagonals have the magic sum. And, like the associative magic squares, every pair of cells symmetrically opposite from the center is a complementary pair. So, a reversible square remains reversible not only under Transform 1 and Transform 2, but by swapping only the described rows or columns. From each even order reversible square, the total number of resulting squares is:

2^n-2(n/2)!²

For odd order, the number is that for order n - 1.

For each of these groups there is one principal reversible square in which:

the top row begins with the numbers 1 and 2
row numbers are in ascending order left to right
column numbers are in ascending order top to bottom

Construction

ReversibleSquares makes principal reversible squares. It uses a simple algorithm to generate all the formats and write the squares in Frénicle standard form in ascending order.

How Many

The numbers of principal reversible squares are given by the OEIS sequence A273013

For any prime number order, there is only one principal reversible square consisting of the sequential numbers.

Orders to 100

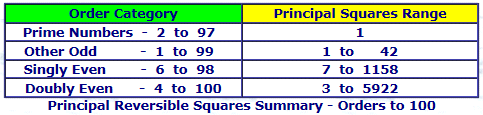
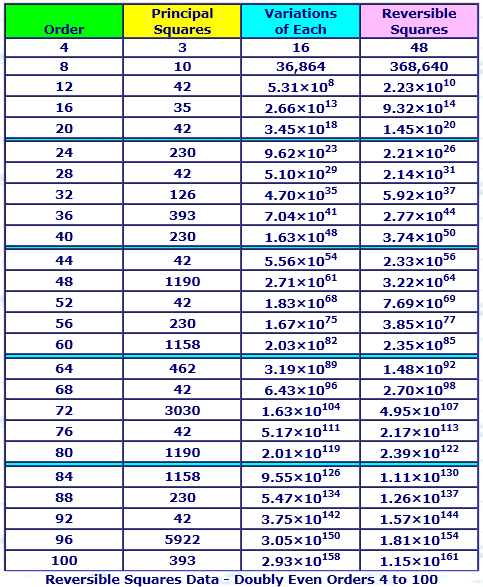
For doubly-even orders, there is a one-to-one correspondence between reversible squares and most-perfect magic squares.

REFERENCES

Heinz, Harvey "Most-perfect Magic Squares" http://recmath.org/Magic%20Squares/most-perfect.htm

Ollerenshaw, Kathleen and David S. Brée "Most-perfect Pandiagonal Magic Squares" http://www.agnesscott.edu/lriddle/women/abstracts/ollerenshaw_mostperfect.htm

Stewart, Ian "Most-Perfect Magic Squares" http://www.klassikpoez.narod.ru/mk/122-123.pdf