Magic Rectangles

Introduction

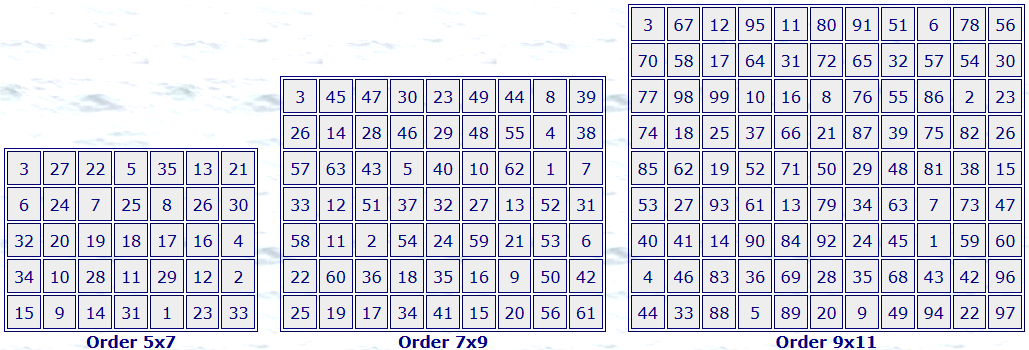
A normal magic rectangle of order r x c contains the integers 1, 2, ..., rc arranged such that the sum of the numbers in each row is the same, and the sum of the numbers in each column is the same:

row sum: c(rc + 1)/2 column sum: r(rc+1)/2

There are no odd by even normal magic rectangles, because for these (rc + 1) is odd; then, if r is odd the column sum is fractional and if c is odd the row sum is fractional.

All unqualified references to magic rectangles on this site mean normal magic rectangles.

Pandiagonal

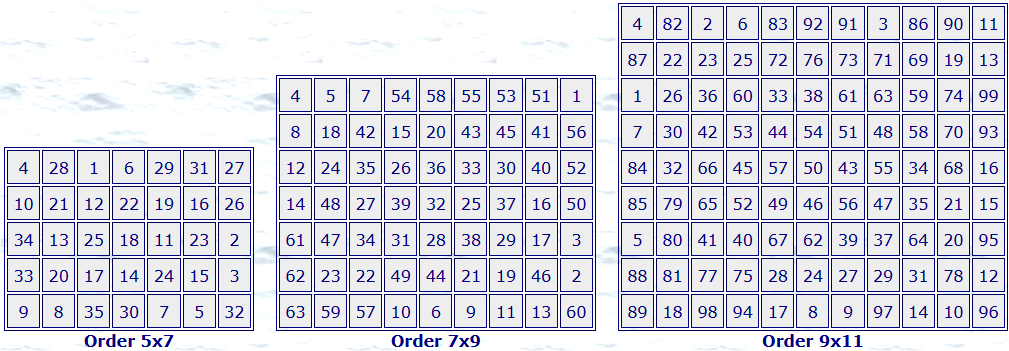
Diagonals are generally not considered in non-square magic rectangles.
However, if diagonals are as shown in the example below, there are 'pandiagonal' magic rectangles for some orders. The diagonal sums are the same as the sums for the shorter of the rows or columns.

4x6 diagonals

Construction

Rectangles of type magic, associative, pandiagonal, and concentric can be made with program MagicRectangles.

Bordered magic rectangles can be made with program BorderedRectangles.

Magic Examples: odd

Orders 3x5, 3x7, 3x9

Boness 3x5, 3x7, 3x9

Magic Examples: even

Orders 2x4, 2x6, 2x8

Bones 2x4, 2x6, 2x8

Associative Examples: odd

Orders 3x5, 3x7, 3x9

Bones 3x5, 3x7, 3x9

Associative Examples: even

Orders 4x6, 4x8, 4x10

Bones 4x6, 4x8, 4x10

Note: To reduce picture width, .5 has been removed from all these bones numbers.

Near-associative Examples: even

Orders 6x10, 6x14

Bones 6x10, 6x14

Note: To reduce picture width, .5 has been removed from all these bones numbers.

Pandiagonal Examples: odd

Orders 5x7, 5x9, 5x11

Bones 5x7, 5x9, 5x11

Pandiagonal Examples: even

Orders 4x6, 4x8, 4x10

Bones 4x6, 4x8, 4x10

Note: To reduce picture width, .5 has been removed from all these bones numbers.

Concentric Examples: odd

Orders 5x7, 7x9, 9x11

Bones 5x7, 7x9, 9x11

Concentric Examples: even

Orders 4x6, 4x8, 4x10

Orders 4x6, 6x8, 8x10

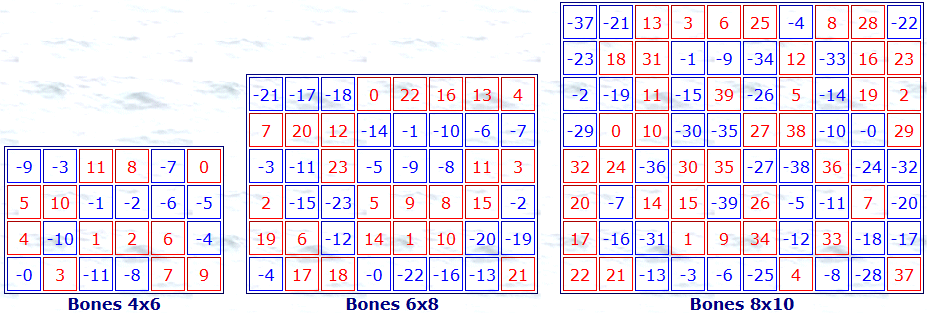
Bones 4x6, 6x8, 8x10

Note: To reduce picture width, .5 has been removed from all these bones numbers.

Bordered Examples: odd

Orders 5x7, 7x9, 9x11

Bones 5x7, 7x9, 9x11

Bordered Examples: even

Orders 4x6, 6x8, 8x10

Bones 4x6, 6x8, 8x10

Note: To reduce picture width, .5 has been removed from all these bones numbers.

REFERENCES

Bhatt, Saurabh and Prof. Ashish Das "Construction of Magic Rectangles"
http://www.math.iitb.ac.in/~ashish/Magic/

Chai, Feng Shun, Ashish Das and Chand Midha
"Construction of magic rectangles of odd order"
http://www.math.iitb.ac.in/~ashish/Magic/paper.pdf

Danielsson, Holger "Book: Magic Rectangles"
https://www.magic-squares.info/info/book-rec.html

De Los Reyes, J. P., Ashish Das, Chand K. Midha and P. Vellaisamy
"On a method to construct magic rectangles of even order"
http://www.math.iitb.ac.in/~ashish/Magic/paper2.pdf

Taneja, Inder J. ijtaneja@gmail.com
"Even Order Magic Squares Using Bordered Magic Rectangles"
https://numbers-magic.com/?p=4292