This page was formerly at:

http://users.eastlink.ca/~sharrywhite/BorderedMagicSquares.html

• Concentric
• Border 5
• How Many
• HP41C
• APL
• Downloads

Bordered Magic Squares

Terminology

This site uses the term Bordered Magic Squares for consecutively concentric magic squares. These have the property that each concentrically inlaid square consists of consecutive integers.

An inlaid square of order m can be converted to a normal magic square by subtracting the (n²+1)/2 of the border order n square and adding (m²+1)/2, which is equivalent to subtracting (n²-m²)/2.

Background

The algorithms here were first programmed on the pocket calculators HP-67 and HP-41CV. The bones numbers are computed and, optionally, (n²+1)/2 added to each number to produce the actual square.

The programs are designed to compute one cell number at a time, given the row and column. A (row, column) is entered to calculate any cell number or, optionally, the square can be stepped through, computing one cell at a time, by repeatedly pressing the R/S button.

Because the squares are not stored in the calculator, the biggest square that can be made is determined by the number computation and display capacities of the calculator, and, time and patience .

Construction

BorderedSquares makes squares from these algorithms. See examples below.
Also, for odd orders, squares are made like those of methods from Holger Danielsson
attributed to Abu'l-Wafa al-Buzjani, Takakazu Seki, Michael Stifel, and J. Travers.

BorderedRectangles also makes these squares and non-square rectangles.

Squares, up to order 32, can also be made below.

Order5Special makes all the order 5 bordered squares. They can also be made on page border 5.

Odd Order Squares

Example Squares: Order 3, 5, 7

The order 3 square can be any aspect of the Lo Shu.

To see the normal magic square of the order 3 square at the center of the order 7 square, subtract (7² - 3²)/2 = 20 from the nested order 3 square numbers. Similarly, subtract (7² - 5²)/2 = 12 for the nested order 5 square. Similarly, subtract (5² - 3²)/2 = 8 for the nested order 3 square of the order 5 square.

Bones of Above Squares

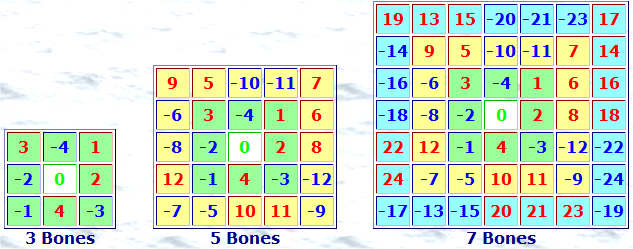
Imagine an X-axis through the center row and a Y-axis through the center column of each bones. A couple of observations:

• bones are nested: order 7 encloses order 5, which encloses order 3, (which encloses order 1)
• the symmetry is apparent:
  • main diagonal numbers are reflected in the center
  • between main diagonals, row numbers are reflected in the X-axis
  • between main diagonals, column numbers are reflected in the Y-axis
  • the sign of the number changes with each reflection

Even Order Squares

Example Squares: Order 6, 8

The center 4x4 square can be any aspect of the 880 order 4 squares.

To see the normal magic square of the order 4 square at the center of the order 8 square, subtract (8² - 4²)/2 = 24 from the nested order 4 square numbers. Similarly, subtract (8² - 6²)/2 = 14 for the nested order 6 square. Similarly, subtract (6² - 4²)/2 = 10 for the nested order 4 square of the order 6 square.

Bones of Above Squares

Note that ½ has been omitted from all the bones numbers displayed here.
Therefore, to convert these displayed bones numbers to the actual square numbers:

• add n²/2 + 1 to the positive numbers
• add n²/2 to the negative numbers

Again, imagine a horizontal X-axis and a vertical Y-axis through the center of each bones. Some observations:

• bones are nested: order 8 encloses order 6, which encloses order 4
• the symmetry is apparent:
  • main diagonal numbers are reflected in the center
  • for the order 4, the other numbers are also reflected in the center
  • except for order 4:
    • between main diagonals, row numbers are reflected in the X-axis
    • between main diagonals, column numbers are reflected in the Y-axis
  • the sign of the number changes with each reflection

Make Squares

Instructions

Click START.

To make a square:

• enter the order
• click OK

To make a bones:

• enter the order
• click the Make Bones box
• click OK

Note: In the bones displayed here, the minus sign is dropped from negative numbers. Positive and negative numbers are distinguished by different colors, (red, blue). Also, ½ is dropped from all numbers for even order bones.

Freeware Disclaimer

The software on this site may be used freely.
You should use only if you agree to the freeware disclaimer.

Please send errata or comments to Harry White, sharrywhite@budshaw.ca

REFERENCES

Danielsson, Holger "Magic Squares" https://www.magic-squares.info/en.html

Heinz, Harvey "Glossary" http://recmath.org/Magic%20Squares/glossary.htm

Nakamura, Mitsutoshi "Magic Cubes and Tesseracts" http://magcube.la.coocan.jp/magcube/en/

Weisstein, Eric W. "Border Square" http://mathworld.wolfram.com/BorderSquare.html

See also: Magic Squares - REFERENCES

Calculators:

Furlow, Warren "The HP-41 Archive Website" http://www.hp41.org/Intro.cfm

Hicks, David G. "The Museum of HP Calculators" http://www.hpmuseum.org/